Varia
... von Ihren Experten für eigentlich eh fast alles.
Corona Mathe
Auch auf die Gefahr hin jetzt ein bissl blöd dazustehen: Ich dachte bis vor Kurzem, dass alles was nicht-linear auch schon exponentiell ist. Also exponentiell wäre „über-linear“ oder halt einfach nur „schneller als linear“. Aber dem ist so nicht.
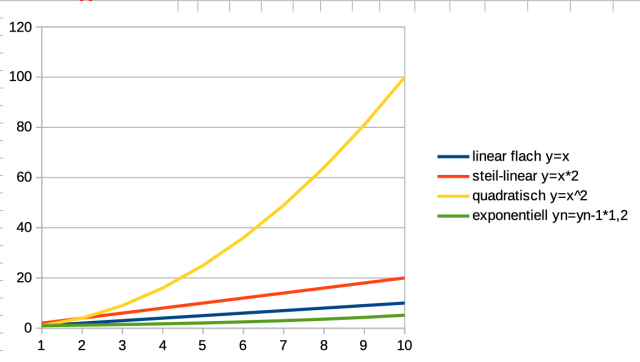
Oben sehen wir vier Kurven zu Funktionen. Die gelbe, quadratische Funktion gibt gleich mal schön Gas und holt schon bei der zweiten Iteration die bis dahin führende steil lineare Funktion (rot) ein. Weit abgeschlagen dümpelt die exponentielle Funktion (grün) dahin - sie ist in diesem Betrachtungsbereich das absolute Schlusslicht.
Die Aufholjagd der exponentiellen Funktion
Wenn wir aber etwas weiter nach vorne rechnen und die Situation nach 30 bis 40 Iterationen ansehen, hat sich das Bild dramatisch verändert: Ab ca. 25 (auf der X-Achse) überholt die exponentielle Kurve die beiden linearen und ab 42 zieht sie auch der bis dahin führenden quadratischen Funktion davon.
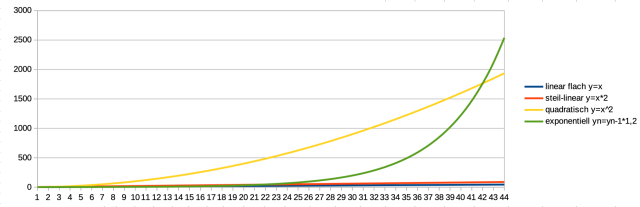
Praktische Bedeutung
Im Alltag haben wir Erfahrung mit linearen Funktionen: „Liebe Kinder, jeder läuft in den Wald und kommt mit zwei Stück Brennholz wieder!“ wär die steil lineare Funktion im Alltag: Es kommen also doppelt so viele Holzstücke zurück, wie Kinder. Auch bei einer sehr großen Kindergruppe laufe ich nicht Gefahr, unter einem Berg an Brennholz begraben zu werden.
Bei quadratischen Funktionen fällt mir schon kaum noch etwas Alltägliches ein: Am ehesten wäre da noch der Kraftstoffverbrauch eines Autos zu nennen, der irgendwie quadratisch also über-linear mit der Geschwindigkeit zunimmt. Oder halt so Sachen wie Lichtstärke und Funkwellen - all das ist aber nur noch wenig greifbar.
Mit exponentieller Vermehrung hatte ich bis vor Kurzem noch gar keine Bekanntschaft gemacht - aber dann kam dieser „COVID“: Da tut sich lange nix - die Experten ziehen sorgenvolle Gesichter doch die Infektionszahlen trödeln gemütlichst vor sich hin. Nur irgendwann ist Schluss mit Trödeln und aus der anfänglich gemütlich-exponentiellen Vermehrung wurde eine explosionsartige. Doch dann ist es im praktischen Leben eigentlich schon wieder zu spät. Man müsste tatsächlich gegensteuern, so lange die Zahlen noch lächerlich niedrig sind.